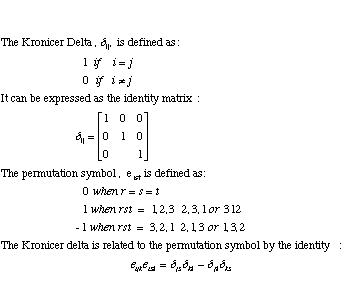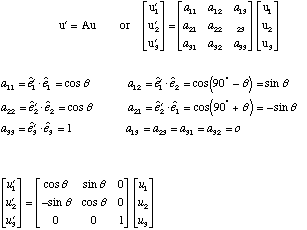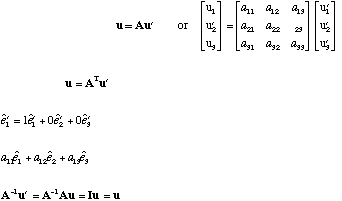A FEW BITS OF MATRIX ALGEBRA
- A vector has both direction and magnitude. It is often denoted by boldface letters u, v, T, F... or by an arrow above the letter.
- A unit vector is a vector of magnitude zero and is denoted by the symbols i, j, k, or by "hat" over letter (which can also denote principal vectors).

Summation conventions:
A repeated (dummy) index i denotes a summation with respect to that index.
Kronecker delta and permutation symbol
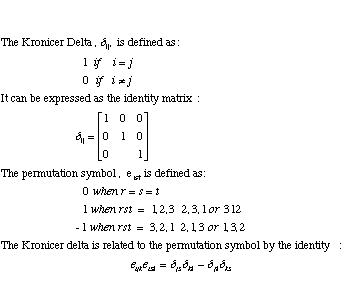
Vector Transformations:
A vector u can be defined in any coordinate system. The vector remains the same regardless of the coordinate system. Matrices can be used to transform a vector from one coordinate system to another coordinate system.
A coordinate system in three dimensions with axes x,y,z can be rotated to a new coordinate system with axes x',y',z'. A vector can be expressed in terms of its' components in the two orthogonal coordinate systems with unit base vectors ê:

The direction cosines form a transformation matrix A. For a counter clockwise rotation around the Z axis the transformation matrix A is:
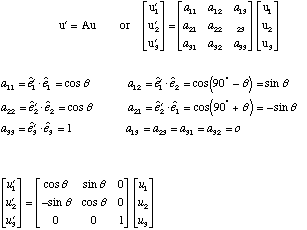
The process can also be reversed. The transformation matrix below is just the transpose of the one above.
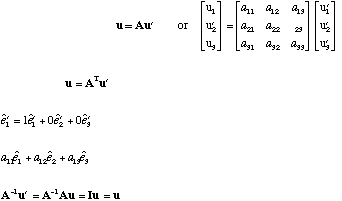
A very nice tool for matrix manipulation is MATLAB© by Mathworks©.
Some useful references:
- Fung, Y.C., A first course in continuum mechanics, 2nd edition, Prentice Hall, 1977.
- Malvern, L.E., Introduction to the mechanics of Continuous Media, Prentice Hall, 713 p, 1969.
- Means, W.G., Stress and Strain, ...
- Ramsay, J.G., and Huber, M.I., Modern Structural Geology -- Volume1, Strain Analysis. Academic Press, New York, 1983.
back to EPS 216 mainpage