
 |
|
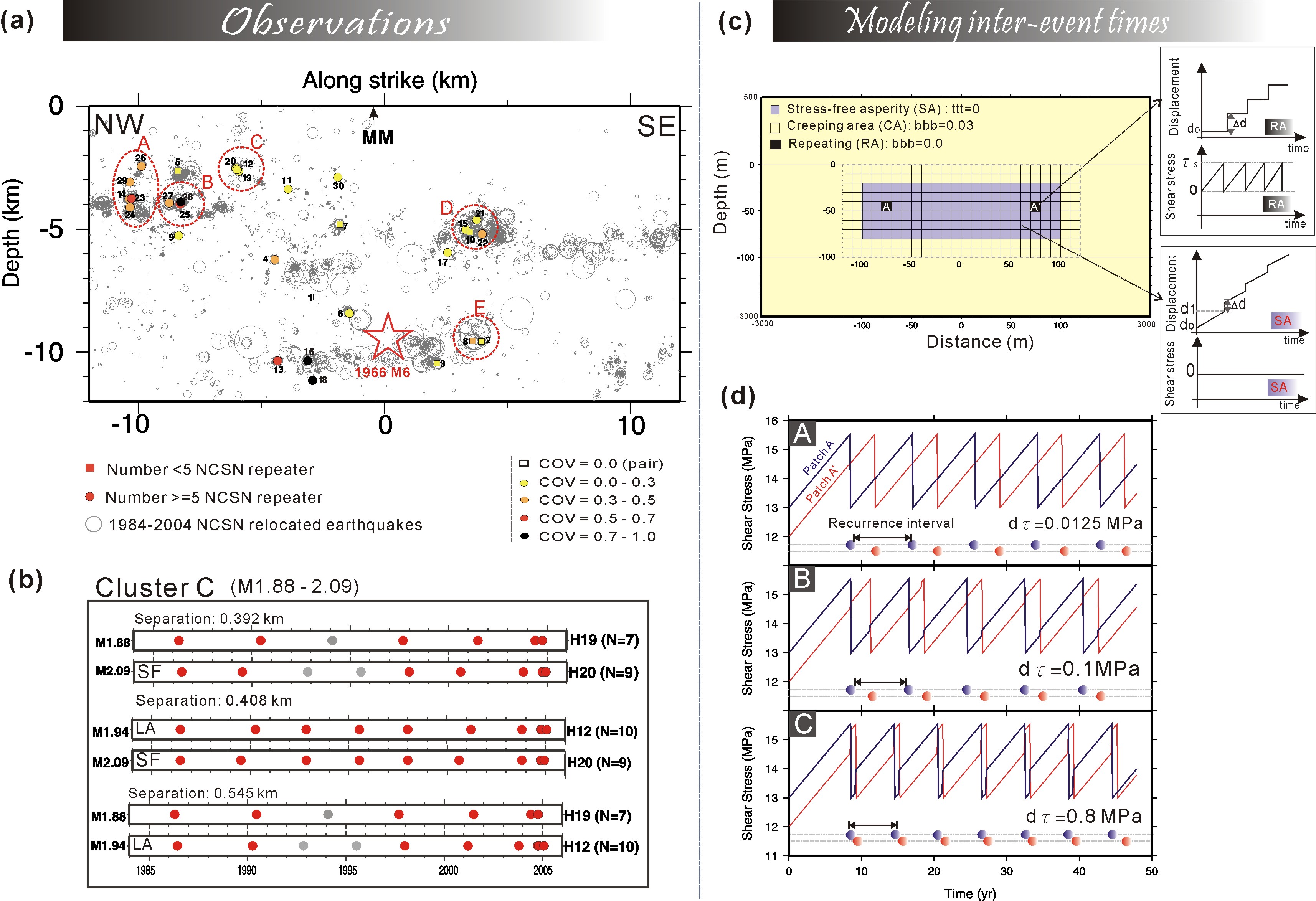
(a)Fault-parallel section showing background seismicity ( grey open circles, relocated seismicity by Waldhauser et al. [2004] and Thurber et al. [2007]) and NCSN-derived repeating sequences (filled circles). Fill color/shades are keyed to the COV in recurrence interval. Open red star indicates the 1966 M6 hypocenter. Dashed red circles indicate the clusters of interest (with inter-repeater distances of less than 1 km). MM indicates the location of Middle Mountain.(b)Event chronology for repeating earthquake sequences in cluster C. The repeating sequences are grouped into pairs with showing their separation in space on the top. Red circles highlight the events with time-separation of less than 1 yr in each pair. (c)(Left) Schematic planar representation of the fault model in cross-section. (Right) Schematic diagrams of stress versus time and displacement versus time at isolated repeatable asperity (RA) and freely slipping zones (SA). In this simplified model, any stress increase due to an asperity rupture is immediately relieved by aseismic slip in creeping area (CA). In our model study we will assume that afterslip decays in a log(t) fashion, consistent with velocity strengthening behavior [Johnson et al., 2006]. (d) Evolution of shear stress of two repeatable asperities. (A)-(C) Stress evolution as a function of stress increment induced by the other rupture (d�n), for two patches have the same size and same stressing rate.
| Project Summary |
What determines the timing of earthquake recurrences
and their regularity is of fundamental importance in understanding the earthquake cycle and has
important implications for earthquake probability and risk estimates. This question cannot be answered
without statistically sufficient observations of recurrence properties in natural earthquake populations.
Following steps are necessary to tend the project towards its successful conclusion: Our preliminary result shows that 67% of quasi-periodic repeating sequences (i.e., coefficient of variation in recurrence interval less than 0.3) correspond to zones of low seismicity, suggesting that these more regular repeating events are more isolated in space and from perturbing stress changes. We find that closely spaced repeating sequences show evidence of strong interaction in time, reflected in temporally clustered event recurrences. The temporal correspondence appears to be a function of separation distance from nearby earthquakes rather than the relative size of the events. The response of the repeating events to the occurrence of larger earthquakes provides the clearest documentation of the interaction process. Accelerations of repeating sequences are associated with M 4 - 5 events that occurred in the mid-1990s and following the Parkfield earthquake when a large number of sequences exhibit accelerated recurrence behavior consistent with rapid afterslip following the mainshock. However, the characteristically decaying afterslip pattern is not obvious for some of the repeating sequences located close to the co-seismic slip area, suggesting either that the stress changes are very heterogeneous, or that the rupture erased or shut off some of the sequence source areas. Building on the above observations, we will be able to develop mechanical models that test the extent to which fault interaction in the form of static stress changes and transient postseismic fault creep produces the observed aperiodicity in the occurrence of these events, and furthermore, attempt to improve predictions of the times of future event repeats.
|
| Tools | Boundary element code Poly3D [Thomas, 1993] for stress modeling |
| Geographic Location | Parkfield, California |
| Group Members Involved |
Kate Huihsuan Chen <Email> <Personal Web Site> Roland Bürgmann Robert Nadeau |
| Project Duration | In Progress (began in 2007) |
| More Information | < ***link description*** > |