DYNAMIC TOPOGRAHY
Some Remarks on Dynamic Topography
Shijie Zhong
Department of Physics, University of Colorado at Boulder, Boulder, Colorado 80309, USA (szhong@colorado.edu)
https://escholarship.org/uc/item/1168t7dh
Introduction
Dynamic topography is the surface deflection caused by traction that mantle convection imparts onto the Earth’s surface. Dynamic topography can affect a number of important surface processes and observables including gravity and topography anomalies, Earth’s surface vertical motions, sea-level change, sedimentations and erosion. Dynamic topography therefore represents an important window into the dynamics of the mantle. While the theory of dynamic topography is well established and understood, the observed dynamic topography (i.e., residual topography) is often not well determined with significant uncertainties. This is because the observed dynamic topography is derived by removing various components of the topography, which are model- dependent. Here, I will present an overview on dynamic topography. I will discuss definitions of dynamic topography, and their historical context. I will discuss all the relevant components of topography including the planetary shape as direct measurements, dynamic topography and model topographies from different processes. I will also focus on the long-wavelength dynamic topography including its amplitude and uncertainties.
Planetary shape and topography
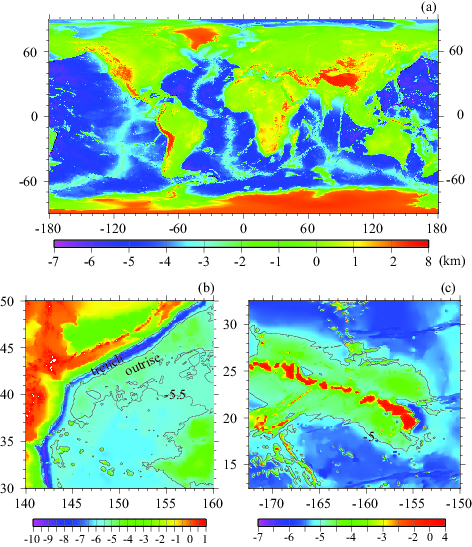
Planetary shape is the solid surface that defines the figure of a planet, while the topography represents the undulation of the planetary solid surface. For a planet with a significant rotation, the rotation leads to an oblate shape. For example, for the Earth, there is a difference of about 21 km between the polar and equatorial radii in this oblateness. However, the rotation-induced oblateness which can be modeled from a hydrostatic theory is often not considered as part of the topography (Fig. 1a). Therefore, the first step to define the topography for a planet is to remove from planetary shape this oblateness. It is helpful to note here that in practice the topography is defined relative to a reference surface of equal gravitational potential that for the Earth corresponds to the mean sea-level. Since the gravitational potential is always defined in a center of mass reference frame, the topography is also defined in this reference frame. Also, because the equi-potential surface (Fig. 2a) tends to have much smaller undulations than the planetary shape, the topography is dominated by the undulations seen in the planetary shape. The Earth’s topography shows high mountains, elevated continents, oceanic islands, depressed ocean floor, mid-ocean ridges, and oceanic trenches (Fig. 1a). The topography is to first order determined by crustal and lithospheric processes. Mountain ranges (e.g., Himalayas) are higher than their surrounding regions because the crust with reduced density than the underlying mantle is thicker in mountainous regions, due to the isostatic compensation process or Airy isostasy [e.g., Watts, 2001]. This theory was firstly proposed based on the lack of gravity anomalies associated with major mountain ranges (Fig. 2a) including the Andes and Himalayas and is clearly supported by seismic observations of crust thickness variations. This is analogous to floated icebergs that emerge above the sea surface due to their smaller density. For the same reason, the elevated continents relative to the sea floor by ~5 km are due to that continental crustal thickness (~35 km) is significantly larger than oceanic crustal thickness (~7 km). The gradual decrease in topography of up to ~3 km from mid-ocean ridges to ocean basins is, however, generally believed to result from gradual decrease in lithospheric temperature, hence increase in lithospheric density due to thermal contraction, from mid-ocean ridges to ocean basins. This is sometimes called Pratt isostasy. However, a couple of seafloor topographic features deserve some discussions. The first is the trench and outer rise topography (Fig. 1b). The trenches can be up to 6 km deeper than their neighboring ocean floor, while outer rises immediately next to trenches show a few hundred meters of topographic higher than their neighboring ocean basins. Trench-outer rise topographies show distinct gravity anomalies (Fig. 2b) [Watts, 2001], suggesting that they are not originated from the crustal or lithospheric density variations, like the other topographic features discussed earlier. The second topographic feature of interest here is the so-called Hawaiian swell topography that is ~1200 km wide, and ~1 km high above the neighboring seafloor with the Hawaiian island chain at its center (Fig. 1c). The broad and gentle swell topography is distinctly different from the localized Hawaiian island chain topography. The swell topography shows less gravity anomalies than those associated with the oceanic islands and trenches but larger gravity anomalies than that associated with mountains of similar size (Fig. 2b). Seismic surveys do not show significant crustal thickness variations associated with the swell topography [e.g., ten Brink and Brocher, 1987]. The observations of gravity anomalies and seismic structure suggest that oceanic trenches and Hawaiian swell topography are caused by other processes that are not associated with crustal compensation as for the mountain ranges. The possible processes include mantle and lithospheric dynamic processes.
Dynamic topography – concept, definitions, and theory
Concept and definition
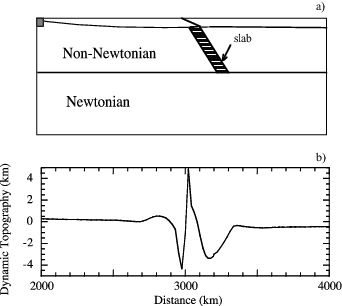
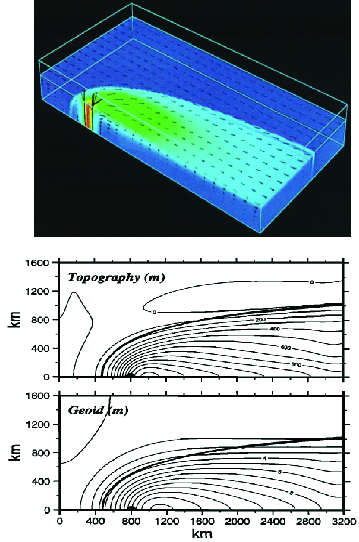
Some discussion on the cause of the trench and outer rise topography and Hawaiian swell topography is instructive before getting into the concept of dynamic topography. Trench and outer rise topography was suggested to result from a vertical load and moment applied at an end of a thin plate (elastic or viscous) [e.g., Watts and Talwani, 1974; De Bremaecker, 1977], although the origin of the load was not clearly stated. The trench topography was also attributed to subduction process in kinematic models with prescribed plate velocity at the surface and in the subducted slab that results in negative pressure above the slab, which causes the surface to depress and hence trench topography [McKenzie, 1969; Melosh and Raefsky, 1980]. Fully dynamic models of subduction zones with negatively buoyant slabs reproduced not only plate motion and subduction but also the negative pressure and trench-like topography in subduction zones [Sleep, 1975]. When a subduction zone thrust fault is considered, dynamic models with slab buoyancy force as driving force explain outer rise, trench and back-arc basin topography seen in subduction zones (Fig. 3) [Zhong and Gurnis, 1994]. Similarly, the Hawaiian swell topography has been attributed to hot, buoyant mantle materials that are originated from a mantle plume beneath the Hawaii hot spot and spread out beneath the Pacific plate [e.g., Olson, 1990; Ribe and Christensen, 1994] (Fig. 4).
In essence, the trench and swell topographic features are originated from mantle convection and plate motion processes, and can be generally called dynamic topography. The significance of dynamic topography and its effect on surface gravity anomalies was first recognized by Pekeris [1935]. This concept has been expanded and applied to many different geophysical and geological problems as to be discussed later. Dynamic topography can be defined as the surface deflection induced by mantle convection. Mantle convection produces variations in pressure and stress in the mantle. At any horizontal density interface such as the Earth’s surface and core- mantle boundary (CMB), the convection-induced stress would lead to a normal force or traction on the interface, and the interface would deform to balance out the normal force, thus resulting in topography at the interface. An operational definition of dynamic topography, h, to the first order, ignoring the self-gravitational effect, can be given as
EQUATION(1)
where Dr is the density difference across the interface (i.e., either the surface or CMB), g is the gravitational acceleration, and s is the radial stress which is related to the pressure p, viscosity rr h and strain rate e by the constitutive equation as EQUATIONINTEXT. For dynamic topography rr with self-gravitational effect which can be important at long-wavelengths, readers may refer Zhang and Christensen [1993] and Zhong et al., [2008].
As to be discussed later, buoyancy in the crust and lithosphere due to either undulation at the Moho or lithospheric thermal structure also produces radial stress s at the surface which rr would lead to the deflection at the surface according to equation (1). Whether such topography induced by buoyancy in the crust and lithosphere can be considered as dynamic topography is still an open question to some researchers. For now, let me simply keep using equation (1) to define dynamic topography, regardless of the source of radial stress or buoyancy. I shall come back to this topic in later sections.
Theory
Generally speaking, a buoyant mantle structure (e.g., a sphere) induces upwelling flow that would lead to a radial stress to cause uplift (or positive topography) at the surface and CMB. A negatively buoyant sphere would have opposite effects to the surface and CMB topography, compared with a buoyant structure. If the Earth’s mantle and crust are treated as viscous fluids, the flow, pressure, stress and dynamic topography induced by any buoyancy in the mantle and crust can be determined by solving the conservation equations of the mass and momentum [e.g., Pekeris, 1935; Hager and Richards, 1989]. The gravity anomalies can then be computed via solving the Poisson’s equation, by considering mass anomalies associated with the buoyancy and dynamic topography at the surface and other density interfaces. Assuming an incompressible fluid, the governing equations are given as [e.g., Hager and Richards, 1989]:
EQUATION (2)
EQUATION (3)
EQUATION (4)
where u is the velocity, dr is the buoyancy, EQUATIONINTEXTis the gravitational potential anomalies, G is the gravitational constant.
These equations were solved to determine dynamic topography and its associated gravity anomalies using different analytic techniques for different mantle convection situation [e.g., Pekeris, 1935; Morgan, 1965]. A spectral-Green’s function method in terms of response functions or kernel functions for dynamic topography and gravity was formulated for Cartesian [Parsons and Daly, 1983] and spherical [Hager, 1984; Richards and Hager, 1984] models. Particularly, together with a propagator matrix technique, this response function method has been proven highly efficient for mantle convection models with one-dimensional viscosity structure (i.e., the viscosity only depends on the depth) [e.g., Hager and Richards, 1989]. However, when three-dimensional mantle viscosity structure exists, numerical solutions (i.e., finite volume and finite element methods) are often required to solve these equations to determine the dynamic topography and gravity anomalies [e.g. Zhong et al., 2007a].
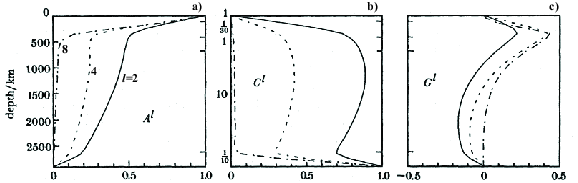
Response functions (or kernels) for dynamic topography and gravity anomalies
The response function solutions help understand how mantle buoyancy source at different depth and wavelength affects the dynamic topography and gravity anomalies, and they also help understand the classical Airy isostasy theory. In this analysis, a localized buoyancy force at a given wavelength (i.e., spherical harmonic degree l and order m) is placed at a given depth or radial location r , that is,
EQUATION (5)
where EQUATIONINTEXT is the delta function, and EQUATIONINTEXT is the spherical harmonic function.
Dynamic topography and the gravity anomalies resulting from this buoyancy can be obtained by solving equations (2)-(4) for a given mantle viscosity structure, using the propagator matrix techniques [Hager and Richards, 1989]. In an example problem presented here that is taken from Hager and Richards [1989], the mantle viscosity is depth-dependent only and the upper mantle and CMB regions are relatively weak. The response functions for surface and CMB dynamic topography and surface geoid anomalies are given as a function of source depth or r for s three harmonic degrees l=2, 4, and 8 in Fig. 5a-5c (note that the wavelengths, which are given by 40000/l km, for l=2 and l=8 are 20000 km and 5000 km, respectively). Notice that the response function for dynamic topography is normalized such that a unit response indicates a perfect 8 compensation at the surface in response to a buoyancy at a depth in equation (5) (Fig. 5a-5b). The response function for the gravity anomalies which is also normalized is given as the geoid response (Fig. 5c).
Surface dynamic topography response is nearly 1 for the delta-function buoyancy near the surface for all three wavelengths (Fig. 5a), indicating that the surface would deform to nearly completely compensate the buoyancy. With the nearly complete compensation for buoyancy at shallow depths, it is not surprising to see near zero geoid response function at these depths (Fig. 5c). Under the viscous flow assumption, the nearly perfect compensation for buoyancy at the surface and shallow depths as seen for l=2, 4 and 8 also occurs for any other shorter wavelengths or larger l. That is, buoyancy associated with undulations of Moho topography would lead to surface topography that compensates the buoyancy. Remarkably, this suggests that the viscous flow theory here predicts the Airy/Pratt isostasy. The surface topography response function decreases rapidly with the depth from one at the surface to zero at the CMB, indicating that the buoyancy at large depths is only partially compensated at the surface and that the buoyancy at the CMB produces zero topography at the surface. Although buoyancy at large depth is only partially compensated at the surface, it also produces dynamic topography at the CMB (Fig. 5b). The CMB topography response function starts from zero at the surface and increases to one at the CMB (Fig. 5b). The topography response functions also depend strongly on wavelength. For example, surface topography response function decreases more rapidly with depths at shorter wavelengths (e.g., at l=8) (Fig. 5a), suggesting that short-wavelength mantle structure at a large depth (e.g., in the lower mantle) is ineffective in producing surface topography.
The geoid response function consists of contributions from three mass anomalies: the internal mass anomaly (i.e., the internal buoyancy), and mass anomalies associated with the induced dynamic topographies at the surface and CMB. While the geoid response function is zero for buoyancy or mass anomaly located at the surface and CMB where the mass anomaly is completely compensated or cancelled by the mass anomaly associated with its induced dynamic topography, the geoid response function is non-zero in the interiors of the mantle because of the partial compensation. In particular, at l=2, the geoid response for the buoyancy in the lower mantle has significant amplitude and has the same sign as the surface topography response function at the same depth. That is, a buoyant (negatively buoyant) mass anomaly in the lower mantle produces surface topography and geoid that are both positive (negative) (Fig. 5a and 5c). However, the geoid response for buoyancy in the upper mantle can have opposite sign from the topography response. Also, the geoid response is nearly zero in the lower mantle at l=8 (Fig. 5c), indicating that the relatively short wavelength geoid is only sensitive to the upper mantle buoyancy. It should be pointed out that the geoid response is quite sensitive to viscosity structure, and such a sensitivity provides a basis to use the geoid modeling to constrain mantle viscosity structure [e.g., Hager and Richards, 1989].
To end this section, it is important to note although the response function from the viscous flow theory predicts the Airy/Pratt isostasy for any wavelengths, gravity and topography observations indicate that topography features at short wavelengths (e.g., oceanic islands and small mountain ranges) are not completely compensated and have significant gravity anomalies [e.g., Watts, 2001]. The viscous flow theory ignores the effects of elastic bending and membrane strengths of the cold and stiff lithosphere. Such effects are strongly dependent on the thickness of the elastic lithosphere [e.g., Turcotte et al., 1981] and can be accounted for by including an elastic shell in the response function theory [Zhong, 2002]. For a typical elastic lithosphere on 9 the Earth (i.e., with thickness <40 km for oceanic lithosphere and tectonically active continental lithosphere or <~100 km for cratonic lithosphere) [e.g., Watts, 2001], the membrane strength effect is generally not important [e.g., Turcotte et al., 1981; Zhong, 2002], but the bending strength may reduce the topographic response significantly at wavelengths less than hundreds of kilometers. However, the viscous flow theory outlined here is generally applicable for analyses of gravity and topography at wavelengths larger than 1000 km for the Earth.
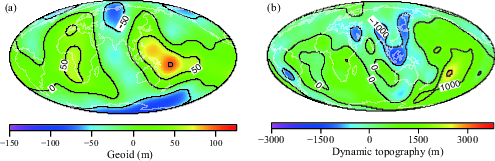
Dynamic topography and long-wavelength geoid anomalies: A global model
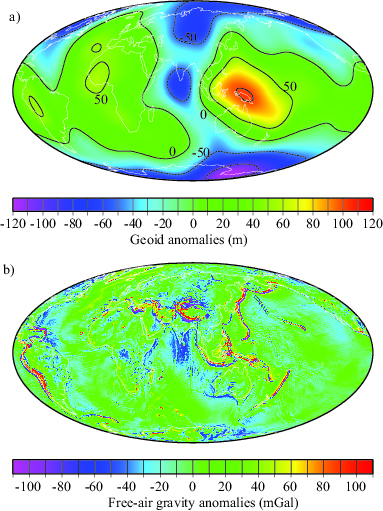
Surface gravity and topography anomalies provide important insights into the rheology and dynamics of the Earth’s mantle and crust. The Earth’s surface has significant gravity anomalies at different scales (e.g., Fig. 2b for the free-air gravity anomalies), but the geoid anomalies are often considered as more effective than gravity anomalies in highlighting long- wavelength features that are relevant to large-scale mantle dynamics (Fig. 2a). An important feature in the Earth’s geoid is its significant power at long-wavelengths with ~75% of the total power at degrees 2 and 3. In particular, the dominant geoid anomalies are the two broad positive anomalies over the central Pacific and Africa (Fig. 2a). Interestingly, the Earth’s mantle also contains similar long-wavelength structures, including seismically slow anomalies in the lower mantle below the Pacific and Africa, and fast anomalies surrounding the Pacific, as seen in all the seismic tomography models (Fig. 2c) [e.g., Dziewonski, 1984; Su et al., 1994; Masters et al., 2000; Houser et al., 2008; Simmons et al., 2010; Ritsema et al., 2011; Panning et al., 2010]. Significant effort has been made since 1980s to understand the origin of the long-wavelength geoid, its connections to the mantle seismic structure and surface volcanism, and its constraint on the mantle viscosity structure [e.g., Hager et al., 1985; Hager and Richards, 1989; Ricard et al., 1993; King and Masters, 1992; Rudolph et al., 2015; Liu and Zhong, 2016], as reviewed recently by Zhong and Liu [2016]. These studies employ mantle flow models as outlined in section 3.2, using seismic structure as a proxy for mantle buoyancy. Dynamic topography is an important 10 byproduct of these geoid models, and its interpretation has been an active area of research in recent years.
Here, I will show a recent example on how the geoid and dynamic topography modeling is done. This example is part of a study from Liu and Zhong [2016]. The viscous flow formulation as outlined in section 3.2 is used. Seismic model SAW642ANb [Panning et al., 2010] is used to derive a model of mantle buoyancy that drives the mantle flow. The top 300 km of the mantle structure is removed from the modeling, as the seismic anomalies at shallow depths may reflect the effects of seismic anisotropy and composition, in addition to thermal effects. Because the geoid is insensitive to the shallow mantle structure (Fig. 5c), ignoring this structure does not have significant effects on the geoid. The viscosity model used here is only depth- dependent with 4 layers: the lithosphere, upper mantle, transition zone and the lower mantle that have non-dimensional viscosity of 20, 7, 0.45, and 50. This viscosity produces the best fit to the geoid with variance reduction of 83.4%, based on thousands of forward modeling calculations [Liu and Zhong, 2016]. The model geoid and dynamic topography at the surface are shown in Fig. 6. The dynamic topography shows no resemblance to the topography, with no elevated continents nor mid-ocean ridge topography, because of the removal of the top 300 km mantle structure. Dynamic topography shows strong long wavelength components, particularly at degree-2, as reflected in the positive topography in the mid-Pacific and African regions and negative topography in Asia, Europe, North Atlantic, and North America. The dynamic topography has ±1 km amplitude.
Other seismic models including Smean [Becker and Boschi, 2002] and S40RTS [Ritsema et al., 2011] have also been attempted in Liu and Zhong [2016], and the results are insensitive to the choice of seismic models. It should be pointed out that different viscosity structures may be obtained by fitting the geoid, depending on how viscosity model is parameterized [e.g., King and Masters, 1992; King, 1995; Rudolph et al., 2015]. However, a robust conclusion appears to be that the top 670 km or 1000 km is weaker than the lower mantle. The resulting dynamic topography is quite similar from these models. However, if the LLSVPs are interpreted as chemically distinct and dense materials, to fit the geoid, the resulting dynamic topography needs to be ~30% larger than that from isochemical mantle models [Liu and Zhong, 2016].
Definitions of dynamic topography – a revisit
Although the term of dynamic topography was used in the response function discussion in sections 3.2 and 3.3 even for buoyancy residing in the lithosphere and crust (e.g., Fig. 5a), there have been debates on how dynamic topography should be defined and a number of different definitions have been proposed in geodynamics literature [e.g., Molnar et al., 2015; Hager and Richards, 1989; Forte et al., 2010; Simmons et al., 2010; Gurnis, 1993a]. Here, I would like to briefly re-visit the definition of dynamic topography.
The first definition considers the topography induced by buoyancy outside of the crust and lithosphere as dynamic topography [e.g., Hager and Richards, 1989]. That is, in this definition, the Tibetan plateau and other major mountain belts with thickened crust or the mid- ocean ridges due to the lithospheric cooling would not be considered as dynamic topography. This is because the topography produced by lithospheric and crustal buoyancy is stationary or static, ignoring crustal or lithospheric deformation, relative to the lithosphere. However, the Hawaiian swell topography would be considered as dynamic topography as its buoyancy source is below the lithosphere (Fig. 4). In practice for computing dynamic topography in the geoid 11 models, as discussed in the last section, any buoyancy above some typical lithospheric depths (e.g., ~200 km) would be ignored. Clearly, in this definition, dynamic topography would not necessarily resemble the observed topography (e.g., no mid-ocean ridges in Fig. 6b [Liu and Zhong, 2016]).

The second definition of dynamic topography considers the topography produced by all the buoyancy including that in the lithosphere as dynamic topography [e.g., Forte et al., 2010; 12 Moucha and Forte, 2011]. Because most of well-constructed mantle seismic tomography models capture some aspects of age-dependent oceanic lithospheric structure (i.e., seismically slower anomalies associated with the younger oceanic lithosphere), mantle flow models using buoyancy derived from these seismic models would lead to >2 km topography from mid-ocean ridges and ocean basins (Fig. 7a from Simmons et al. [2010]). As global seismic tomography models often exclude crustal structure, modeled dynamic topography in continental areas without the crust are depressed rather than elevated, as expected (Fig. 7a). The overall peak-to-peak dynamic topography may exceed 4 km using this definition.
There is no fundamental difference between these two definitions for dynamic topography. The inclusion of buoyancy in the top 200-300 km in the second definition is the only difference from the first definition. Because the long-wavelength geoid is rather insensitive to buoyancy at shallow depths (see Fig. 5c), these two approaches would give similar long- wavelength geoid anomalies. However, because surface dynamic topography is sensitive to buoyancy at shallow depths (Fig. 5a), the second approach for dynamic topography would give rise to relatively large amplitude of dynamic topography such as >2 km mid-ocean ridge topography that is controlled by shallow mantle structures. This makes it more difficult to see dynamic topography induced by deep mantle structure that is of a smaller amplitude and is also largely responsible for the geoid anomalies. Additionally, it is generally believed that the shallow mantle seismic structure may contain relatively large effects from composition and seismic anisotropy than the deep mantle structure, making it harder to convert seismic anomalies to density anomalies or buoyancy [e.g., Simmons et al., 2010; Hager and Richards, 1989]. However, as seismic models are improved, including the shallow mantle structure in mantle dynamic models would lead to important insights into surface tectonics and other observations [e.g., Moucha and Forte, 2011]. Interested readers can find more discussions on these two different definitions of dynamic topography in Molnar et al. [2015] and Gurnis [1993a].
Molnar et al. [2015] proposed that dynamic topography needs to be estimated on the basis of free-air gravity anomalies. Their discussion is mainly on topographic features in continental regions on a relatively small length-scale (<~3000 km or l>12). Molnar et al. [2015] recognized the same underlining physics presented in sections 3.2-3.3, although their analyses were done in Cartesian geometry ignoring the effects of the CMB, which is appropriate for the regional scale problems they considered. While correctly characterizing the difference between the above-mentioned two definitions of dynamic topography, Molnar et al. [2015] suggested an operational definition of dynamic topography, that is, to estimate dynamic topography based on the free-air gravity anomalies, using admittance of ~50 mgal/km. They further suggested that the dynamic topography in most continental regions including western US, southern Africa, and eastern Asia would not exceed 300 meters. However, this conclusion cannot be simply extrapolated to longer wavelength dynamic topography, because the admittance or geoid- topography response function is strongly dependent on the depth of buoyancy force [e.g., Liu and Zhong, 2016; Colli et al., 2016]. This can also be seen in Fig. 5a and 5c, given that the geoid response function can be positive or negative, while the surface topography is always positive.
Observations of dynamic topography
In this section, I will discuss dynamic tomography from an observational point of view. More specifically, I will describe how the dynamic topography may be derived from observations for the present-day Earth and how it may be inferred from geological records for the Earth’s past.
Present-day dynamic topography and residual topography
The geoid modeling studies predict ±1 km long-wavelength dynamic topography (i.e., using the first definition or the dynamic topography caused by sublithospheric mantle structure) with positive topography in the Pacific and Africa (Fig. 6b) [e.g., Hager et al., 1985; Hager and Richards, 1989], as discussed in section 4. An important question has been whether there is any observational evidence for these dynamic topography features. As discussed in sections 2 and 3, the Hawaiian swell topography is on a length-scale of ~1000 km and is suggested to result from plume-derived hot, buoyant mantle materials that spread below the Pacific plate (Fig. 4). It has been recognized that much of the western and central Pacific, including the Darwin Rise [Menard, 1964] and French Polynesia [McNutt and Fischer, 1987] regions, also has significantly shallower ocean depths than expected for its lithospheric age. This shallower-than-expected topographic feature was called as the Pacific “superswell” [McNutt and Fischer, 1987]. It was also recognized that southern Africa and its adjacent regions may have unusually high topography [Nyblade and Roberson, 1994; Lithgow-Bertelloni and Silver, 1998]. Both the Pacific superswell and African topographic high were suggested to have a deep mantle origin [McNutt and Judge, 1990; Lithgow-Bertelloni and Silver, 1998].
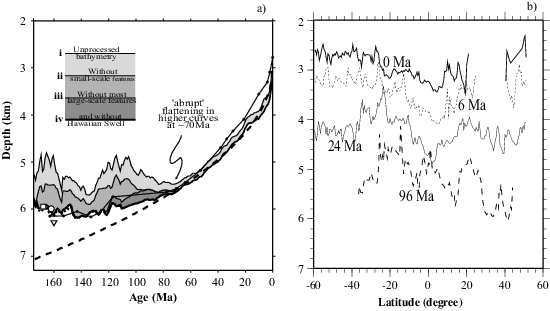
However, inferring dynamic topography is not straightforward due to a number of complicating factors. As discussed earlier, continental topography is mostly controlled by crustal and lithospheric structures, while seafloor topography is mainly controlled by thermal isostasy of lithospheric thermal structure which is determined by cooling process or lithospheric age [Parsons and Sclater, 1977]. To infer dynamic topography (i.e., in its first definition), topography resulting from these shallow structure needs to be removed, and dynamic topography is also called “residual topography”. The complexity in continental crustal and lithospheric thermal and compositional structures makes it difficult to assess their contributions to the topography, and hence the residual topography in continental regions contains significant uncertainties [e.g., Molnar et al., 2015]. In oceanic regions, while crustal structure is relatively simple except for oceanic plateaus, there have been debates on how seafloor topography depends on the age of lithosphere [e.g., Parsons and Sclater, 1977; Marty and Cazenave, 1989]. Ocean depth (i.e., seafloor topography) generally increases with lithospheric age following closely the prediction of the cooling half-space model until the age reaches to 70-80 Ma, and for older seafloor, ocean depth does not increase as much with the age (i.e., “flattening”) (Fig. 8a) [e.g., Parsons and Sclater, 1977; Stein and Stein, 1992; Hillier and Watts, 2005; Crosby et al., 2006]. The observed ocean depth-age relationship is often modeled by the so-called plate model. However, the plate models can differ significantly from each other, depending on whether sediments and seamounts are removed properly considered (Fig. 8a) [e.g., Hillier and Watts, 2005; Zhong et al., 2007].
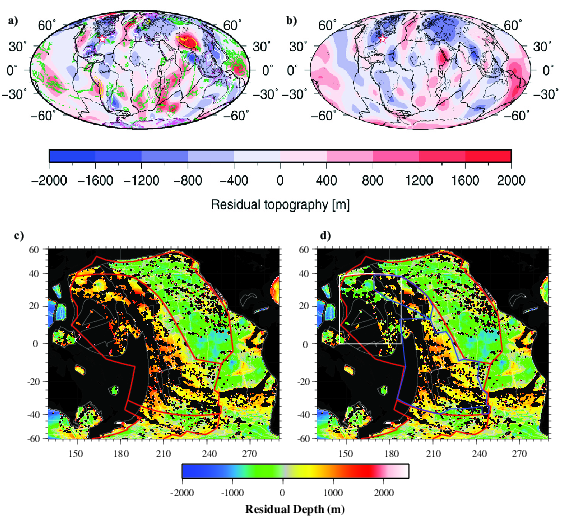
Most of the recent studies on residual topography use some forms of plate model for ocean depth-age relationship as a reference (Fig. 9a and 9b) [e.g., Flament et al., 2013; Steinberger, 2007]. Although the long-wavelength patterns in residual topography between Fig. 9a and 9b are similar, noticeable differences exist on regional scales (<4000 km in length scales in North Pacific, Tibet plateau, and east of Australia), because different plate models and crustal structures were used. Some studies also considered the half-space cooling model as the reference in determining residual topography [Davies and Pribac, 1993; Panasyuk and Hager, 2000]. Using predicted seafloor topography from the half-space cooling model or plate model as reference would lead to very different residual topography (Fig. 9c and 9d) [Panasyuk and Hager, 2000; Zhong et al., 2007]. With the half-space cooling model as a reference, the residual topography shows > 1 km for relatively old seafloor in the western Pacific (Fig. 9c). However, using the plate model as the reference, the residual topography has a much smaller amplitude as expected (Fig. 9d), because the plate model fits the observed topography-age relation. As pointed out by Davies and Pribac [1993] and to be discussed later, it is unclear whether a plate model or half- space cooling model should be used as a reference to determine residual topography.
Inferring residual topography in oceanic regions is also complicated by surface features including seamounts (e.g., Fig. 9c shows seamounts in the western and central Pacific as documented by Wessel [2001]) and sediments (e.g., near continental passive margins off Africa and Americas). The effects of seamounts and sediments are considered in some recent studies on ocean depth-age relations in the Pacific by using filters [e.g., Hiller and Watts, 2005] or simple removal of seamounts [Zhong et al., 2007]. Removal of seamounts reduces topographic “flattening” at old seafloor, but the topography remains significantly less than the prediction from the half-space cooling model (Fig. 8a) [Hiller and Watts, 2005; Zhong et al., 2007].
There have been a number of recent efforts in constructing residual topography, using updated dataset for crustal and lithospheric structures [e.g., Hoggard et al., 2016; Steinberger, 2016]. However, the residual topography in continental regions likely suffers the same uncertainty problem as in previous studies because of the uncertainties in crustal and lithospheric structures, as pointed out by Molnar et al. [2015]. The most significant issue with the residual topography on the seafloor remains what the reference model is to use for correcting the thermal isostasy. For example, Hoggard et al. [2016] concluded that the amplitude of long-wavelength topography is less than 0.5 km, using the plate model like ocean depth-age relation from Crosby et al., [2006]. However, if the ocean depth-age relation in Crosby et al., [2006] already contains some signals from the dynamic topography caused by the mantle buoyancy, then its removal essentially means that part of the dynamic topography signals may have also been removed from the residual topography.
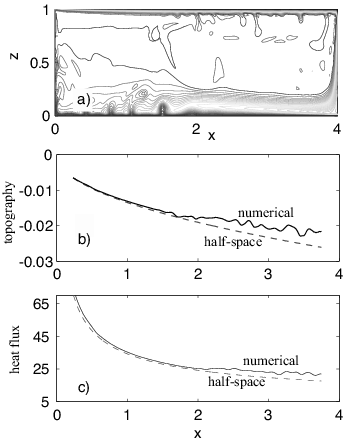
At this point, it is worthwhile to discuss the plate model and half-space cooling model. The plate model is basically an empirical model designed to fit the observed ocean depth-age relation (Fig. 8a), assuming that the only controlling factor is the lithospheric thermal structure or age [Parsons and Sclater, 1977]. The plate model assumes a constant mantle temperature at the base of the lithosphere, and plate thickness and other parameters are obtained by fitting the observed ocean depth-age relation [e.g., Stein and Stein, 1992]. Although the plate model is simple, its physical basis has always been in question. Sub-lithospheric small-scale convection was proposed as the physical basis for the plate model [Parsons and McKenzie, 1978], but O’Connell and Hager [1980] argued that because the topography is sensitive to both lithospheric and mantle thermal structure, the small-scale convection, by enhancing the cooling of the mantle below the lithosphere, may lead to more subsidence at the old lithosphere rather than topographic flattening. In modeling sub-lithospheric small-scale convection, Huang and Zhong [2005] found that while the sub-lithospheric mantle may help maintain approximately constant temperature, the resulting surface topography is between the predictions from the plate model and half-space cooling model (Fig. 10). This suggests that the half-space cooling and plate models are the two end-member cases for describing the lithospheric thermal structure and that residual topography inferred using these models likely represents the upper and lower bounds of dynamic topography in oceanic regions.
It is also important to recognize that lithospheric age is not the only control on seafloor topography. This is evident by ~1 km topographic variations along the mid-ocean ridge where the age is uniformly zero, as pointed out by Marty and Cazenave [1989], which should be viewed as evidence for dynamic topography [Davies and Pribac, 1993]. Fig. 8b shows topographic profiles for ages: 0, 6, 24, and 96 Ma in the Pacific plate [Zhong et al., 2007], and note ~1 km topographic variations over relatively large length scales.
The long-wavelength dynamic topography including ~1 km topographic highs in the Pacific and Africa associated with the geoid modeling appears to be consistent with the inferred dynamic topography, although inferring dynamic topography is always difficult with significant uncertainties [e.g., Molnar et al., 2015]. The inferred <0.5 km long-wavelength dynamic topography in the Pacific [Hoggard et al., 2016] may only represent a lower bound on the dynamic topography, and it is unlikely that such a small dynamic topography can explain the long-wavelength geoid/gravity anomalies. Although modeling the geoid and free-air anomalies is equivalent in mantle flow models [Liu and Zhong, 2016], free-air anomalies provide more restrictive constraints on intermediate length scales [Forte et al., 2010; Liu and Zhong, 2016]. To improve the modeling of dynamic topography and gravity anomalies at these intermediate length scales is an important task for future studies [e.g., Moucha et al., 2009]. This would also require better seismic models on regional scales.
Observational evidence for dynamic topography in geological history
One appealing evidence for dynamic topography is from the history of large-scale vertical motion of continents including continental flooding as recorded in stratigraphy and global sea- level change. A comprehensive review on the topic can be found in Flament et al. [2013], and I will just give a brief discussion on some more recent development.
Subduction process was suggested to affect development of sedimentation and stratigraphic sequences by Cross and Pilger [1978]. Models of subduction was formulated to quantify dynamic topography in the overriding plate to explain the continental flooding in North America in Cretaceous by Mitrovica et al. [1989]. Similar models of subduction were proposed to account for continental flooding in other places in Phanerozoic [Gurnis, 1993b; Burgess et al., 1997; Liu et al., 2008]. More recent studies employ plate motion history in convection models to predict dynamic topography history in different regions to account for observations related to vertical motions including stratigraphy, sedimentation, and erosion [Gurnis et al., 1998; Lithgow- Bertelloni and Gurnis, 1997; Moucha and Forte, 2011; Moucha et al., 2008; Liu et al., 2008; Shephard et al., 2010; Zhang et al., 2012; Flowers et al., 2012]. Dynamic topography provides a useful concept and framework to understand these large-scale continental flooding events seen in stratigraphic sequences even in tectonically stable cratonic regions that are difficult to explain by other mechanisms including eustatic sea-level change. Flowers et al., [2012] show that un- roofing and burial processes as revealed from studies of thermochronology may also potentially provide constraints on dynamic topography and mantle dynamic process. Brune [2010] suggests that history of dynamic topography on regional scales may have significant effects on erosion processes that may potentially open new research directions to related mantle dynamics to geomorphology.
Concluding remarks
Dynamic topography results from traction on the lithosphere from mantle convection. Dynamic topography should exist at different wavelengths and different amplitudes that are controlled by the dynamics of mantle. Dynamic topography may have important effects on a number of observations including the gravity and topography anomalies, vertical motion history of continents, sea-level change, sedimentation and erosion processes on the Earth’s surface. Although different definitions of dynamic topography exist in the literature, the theory of dynamic topography is well established and understood. Modeling the long-wavelength geoid anomalies suggests up to ±1 km long-wavelength dynamic topography for the present-day Earth. While this predicted dynamic topography is consistent with dynamic (residual) topography inferred from observations, there are still significant uncertainties in the inferred dynamic topography, mainly because the crustal and lithospheric thermal and compositional structures to which the topography is sensitive are not well constrained. However, by interacting with surface processes, dynamic topography provides an important window to explore the dynamics of the mantle. Together with better seismic imaging of crustal and mantle structure and characterizing crustal and mantle chemical and physical properties, dynamic topography will continue playing an important role in geodynamics studies.
References
Becker, T.W., Boschi, L. (2002), A comparison of tomographic and geodynamic mantle models. Geochem. Geophys. Geosystems 3, 1003. doi:10.1029/2001GC000168
Braun, J. (2010), The many surface expressions of mantle dynamics, Nat. Geosci., 3, 825–833
Burgess, P.M., Gurnis, M., and Moresi, L. (1997), Formation of sequences in the cratonic interior of North America by interaction between mantle, eustatic, and stratigraphic processes: Geological Society of America Bulletin, v. 109, no. 12, p. 1515–1535, doi:10.1130/0016-7606.
Colli, L., Ghelichkhan, S. & Bunge, H.-P. (2016), On the ratio of dynamic topography and gravity anomalies in a dynamic Earth. Geophys. Res. Lett. 43, 2510-2516.
Crosby, A. G., McKenzie, D. P. & Sclater, J. G. (2006), The relationship between depth, age and gravity in the oceans. Geophys. J. Int. 166, 553-573.
Cross, T. A., and Pilger, R. H. (1978), Tectonic controls of Late Cretaceous sedimentation, western interior, U.S.A.: Nature, v. 274, p. 653–657
Davies, G. F., and F. Pribac (1993), Mesozoic seafloor subsidence and the Darwin Rise, past and present, in The Mesozoic Pacific: Geology, Tectonics, and Volcanism, Geophys. Monograph. Ser., vol. 77, edited by M. S. Pringle et al., pp. 39–52, AGU, Washington, D. C.
De Bremaecker, J.-C. (1977), Is the oceanic lithosphere elastic or viscous? J. Geophys. Res., 82, 2001-2004.
Dziewonski, A. (1984), Mapping the Lower Mantle - Determination of Lateral Heterogeneity in P-Velocity up to Degree and Order-6. J. Geophys. Res. 89, 5929–5952.
Flament, N., M. Gurnis, and R. D. Müller (2013), A review of observations and models of dynamic topography, Lithosphere, 5, 189–210, doi:10.1130/L245.1
Flowers, R.M., Ault, A.K., Kelley, S.A., Zhang, N., Zhong, S. (2012), Epeirogeny or eustasy? Paleozoic-Mesozoic vertical motion of the North American continental interior from thermochronometry and implications for mantle dynamics. Earth Planet. Sci. Lett. 317, 436–445. doi:10.1016/j.epsl.2011.11.015
Forte, A., S. Quéré, R. Moucha, N. A. Simmons, S. P. Grand, J. X. Mitrovica, and D. B. Rowley (2010), Joint seismic-geodynamic-mineral physical modelling of African geodynamics: A reconciliation of deep-mantle convection with surface geophysical constraints, Earth Planet. Sci. Lett., 295, 329–341.
Gurnis, M. (1993a), Comment on “Dynamic surface topography: A new interpretation based upon mantle flow models derived from seismic tomography,” by A.M. Forte, W.R. Peltier, A.M.
Dziewonski, and R.L. Woodward: Geophysical Research Letters, v. 20, no. 15, p. 1663–1664, doi:10.1029/93GL01489
Gurnis, M. (1993b), Phanerozoic marine inundation of continents driven by dynamic tomography above subducting slabs, Nature, 364, 589–593.
Gurnis, M., Müller, R.D., and Moresi, L. (1998), Cretaceous vertical motion of Australia and the Australian Antarctic Discordance: Science, v. 279, no. 5356, p. 1499–1504, doi:10.1126/science.279.5356.1499.
Hager, B. (1984), Subducted slabs and the geoid: Constraints on mantle rheology and flow, J. Geophys. Res., 89(B7), 6003–6015, doi:10.1029/JB089iB07p06003.
Hager, B.H. and Richards, M.A. (1989), Long-wavelength variations in Earth’s geoid - physical models and dynamical implications, Phil. Trans. R. Soc. Lond., Ser. A, 328, 309–327.
Hager, B.H., Clayton, R.W., Richards, M.A., Comer, R.P., Dziewonski, A.M. (1985), Mantle heterogeneity, dynamic topography and the geoid, Nature, 313, 541-545
Houser, C., Masters, G., Shearer, P., Laske, G. (2008), Shear and compressional velocity models of the mantle from cluster analysis of long-period waveforms, Geophys. J. Int., 174, 195-212.
Hillier, J. K. and Watts, A. B. (2005), Relationship between depth and age in the North Pacific Ocean, J. Geophys. Res., 110, B02405, doi:10.1029/2004JB003406.
Hoggard, M.J., N. White, and D. Al-Attar (2016), Global dynamic topography observations reveal limited influence of large-scale mantle flow, doi:10.1038/NGEO2709, Nature-Geoscience.
Huang, J.S., Zhong, S.J. (2005), Sublithospheric small-scale convection and its implications for residual topography at old ocean basins and the plate model, J. Geophys. Res., 110, B05404, 10.1029/2004JB003153
King, S. D. (1995). Radial models of mantle viscosity: results from a genetic algorithm. Geophys. J. Int., 122: 725–734. doi: 10.1111/j.1365-246X.1995.tb06831.x
King, S. D., and G. Masters (1992), An inversion for radial viscosity structure using seismic tomography, Geophys. Res. Lett., 19, 1551–1554.
Lithgow-Bertelloni, C., Silver, P.G. (1998), Dynamic topography, plate driving forces and the African superswell. Nature 395, 269–272. doi:10.1038/26212
Liu, L.J., Spasojevic, S., Gurnis, M. (2008), Reconstructing Farallon Plate Subduction Beneath North America Back to the Late Cretaceous. Science 322, 934–938. doi:10.1126/science.1162921
Liu, X., and S. Zhong (2016), Constraining mantle viscosity structure for a thermochemical mantle using the geoid observation, Geochem. Geophys. Geosyst., 17, 895–913, doi:10.1002/2015GC006161.
Marty, J. C., and A. Cazenave (1989), Regional variations in subsidence rate of oceanic plates: A global analysis, Earth Planet. Sci. Lett., 94, 301-315.
Masters, G., Laske, G., Bolton, H., Dziewonski, A. (2000), The Relative Behavior of Shear Velocity, Bulk Sound Speed, and Compressional Velocity in the Mantle: Implications for Chemical and Thermal Structure, in: Karato, S.-I., Forte, A., Liebermann, R., Guysters,
Stixrude, L. (Eds.), Earth’s Deep Interior: Mineral Physics and Tomography From the Atomic to the Global Scale. American Geophysical Union, pp. 63–87.
McKenzie, D.P. (1969), Speculation on the consequences and causes of plate motions, Geophys. J. R. Astron. Soc., 18, 1-23.
McNutt, M. K., and K. M. Fischer (1987), The South Pacific superswell, in Seamounts, Islands, and Atolls, Geophys. Monogr. Ser., vol. 43, edited by B. H. Keating et al., pp. 25–34, AGU, Washington, D. C.
McNutt, M. K., and A. V. Judge (1990), The Superswell and mantle dynamics beneath the South Pacific, Science, 248, 969–975.
Melosh, H.J., and A. Raefsky (1980), The dynamical origin of subduction zone topography, Geophys. J. R. Astron. Soc., 60, 333-354.
Menard, H. W. (1964), Marine Geology of the Pacific, 271 pp., McGraw-Hill, New York. Mitrovica, J. X., C. Beaumont, and G. T. Jarvis (1989), Tilting of continental interiors by the dynamical effects of subduction, Tectonics, 8(5), 1079–1094, doi:10.1029/TC008i005p01079.
Molnar, P., P. C. England, and C. H. Jones (2015), Mantle dynamics, isostasy, and the support of high terrain. J. Geophys. Res. Solid Earth, 120, 1932–1957. doi: 10.1002/2014JB011724
Morgan, W. J. (1965), Gravity anomalies and convection currents: 1. A sphere and a cylinder sinking beneath the surface of a viscous fluid, J. Geophys. Res., 70, 6175–6187, doi:10.1029/JZ070i024p06175.
Moucha, R., and A. M. Forte (2011), Changes in African topography driven by mantle convection, Nat. Geosci., 4, 660–661.
Moucha, R., A. M. Forte, D. B. Rowley, J. X. Mitrovica, N. A. Simmons, and S. P. Grand (2008), Mantle convection and the recent evolution of the Colorado Plateau and the Rio Grande Rift valley, Geology, 36, 439–442.
Moucha, R., A. M. Forte, D. B. Rowley, J. X. Mitrovica, N. A. Simmons, and S. P. Grand (2009), Deep mantle forces and the uplift of the Colorado Plateau, Geophys. Res. Lett., 36, L19310, doi:10.1029/2009GL039778.
Nyblade, A. A., and S. W. Robinson (1994), The African superswell, Geophys. Res. Lett., 21, 765–768.
O’Connell, R. J. and Hager, B. H. (1980), On the thermal state of the Earth. in: Physics of the Erath’s Interior, edited by A. Dziewonski and E. Boschi, pp. 270– 317, Elsevier, New York.
Olson, P. (1990), Hot spots, swells and mantle plumes, Magma Transport and Storage, edited by M. P. Ryan, pp. 33-51, John Wiley, New York.
Panasyuk, S. V., and B. Hager (2000), Models of isostatic and dynamic topography, geoid anomalies, and their uncertainties. J. Geophys. Res., 105(B12), 28199–28209
Panning, M. P., V. Lekic, and B. A. Romanowicz (2010), The importance of crustal corrections in the development of a new global model of radial anisotropy. J. Geophys. Res., 115, B12325
Parsons, B., and S. F. Daly (1983), The relationship between surface topography, gravity anomalies and temperature structure of convection, J. Geophys. Res., 88, 1129-1144.
Parsons, B. and McKenzie, D. (1978), Mantle convection and thermal structure of the plates, J. Geophys. Res., 83, 4485-4496.
Parsons, B., and J. G. Sclater (1977), An analysis of the variation of the ocean floor bathymetry and heat flow with age, J. Geophys. Res., 82, 803–827.
Pekeris, C.L. (1935), Thermal convection in the interior of the Earth: Geophysical Journal International, v. 3, p. 343–367, doi:10.1111/j.1365-246X.1935.tb01742.x.
Ribe, N. M. and Christensen, U. R. (1994), Three-dimensional modeling of plume-lithosphere interaction, J. Geophys. Res., 99,669-683.
Ricard, Y., M. A. Richards, C. Lithgow-Bertelloni, and Y. Lestunff (1993), A geodynamic model of mantle density heterogeneity, J. Geophys. Res., 98, 21,895–21,909.
Richards, M.A., and B. H. Hager (1984), Geoid anomalies in a dynamic Earth, J. Geophys. Res., 89, 5987-6002.
Ritsema, J., A. Deuss, H. J. van Heijst, and J. H. Woodhouse (2011), S40RTS: A Degree-40 Shear-Velocity Model For The Mantle From New Rayleigh Wave Dispersion, Teleseismic Traveltime And Normal-Mode Splitting Function Measurements. Geophys. J. Int. 184 (3):1223-1236.doi: 10.1111/j.1365-246X.2010.04884.x.
Rudolph, M. L., V. Lekic´, and C. Lithgow-Bertelloni (2015), Viscosity jump in Earth’s mid-mantle, Science, 350(6266), 1349–1352, doi:10.1126/science.aad1929
Shephard, G.E., Müller, R.D., Liu, L., and Gurnis, M. (2010), Miocene drainage reversal of the Amazon River driven by plate-mantle interaction: Nature Geoscience, v. 3, no. 12, p. 870–875, doi:10.1038/ngeo1017.
Simmons, N. A., A. M. Forte, L. Boschi, and S. P. Grand (2010), GyPSuM: A joint tomographic model of mantle density and seismic wave speeds, J. Geophys. Res., 115, B12310, doi:10.1029/2010JB007631
Sleep, N.H. (1975), Stress and flow beneath island arcs, Geophys. J. R. Astron. Soc., 42, 827-857.
Stein, C. A., and S. Stein (1992), A model for the global variation in oceanic depth and heat flow with lithospheric age, Nature, 359, 123–129.
Steinberger, B. (2016), Topography caused by mantle density variations: observation-based estimates and models derived from tomography and lithosphere thickness, Geophys. J. Int., 205, 604–621.
Steinberger, B. (2007), Effects of latent heat release at phase boundaries on fl ow in the Earth’s mantle, phase boundary topography and dynamic topography at the Earth’s surface: Physics of the Earth and Planetary Interiors, v. 164, no. 1–2, p. 2–20, doi:10.1016/j.pepi.2007.04.021.
Su, W., Woodward, R., Dziewonski, A. (1994), Degree-12 Model of Shear Velocity Heterogeneity in the Mantle. J. Geophys. Res.-Solid Earth 99, 6945–6980. doi:10.1029/93JB03408.
ten Brink, U. S., and Brocher, T. M. (1987), Multichannel seismic evidence for a subcrustal intrusive complex under Oahu and a model for Hawaiian volcanism, J. Geophys. Res., 92, 13,687-13,707.
Turcotte, D. L., R. J. Willemann, W. F. Haxby, & J. Norberry (1981), Role of membrane stresses in the support of planetary topography, J. Geophys. Res., 86, 3951-3959.
Watts, A.B. (2001). Isostasy and Flexure of the Lithosphere, 472pp, Cambridge University Press, Cambridge.
Watts, A. B. and Talwani, M. (1974), Gravity anomalies seaward of deep-sea trenches and their tectonic implications, Geophys. J. R. Astron. Soc., 36, 57-90.
Wessel, P. (2001), Global distribution of seamounts inferred from gridded Geosat/ERS-1 altimetry, J. Geophys. Res., 106, 19,431-19,441.
Zhang, S. X., and U. Christensen (1993), Some effects of lateral viscosity variations on geoid and surface velocities induced by density anomalies in the mantle. Geophys. J. Int., 114, 531–547.
Zhang, N., Zhong, S., Flowers, R.M. (2012), Predicting and testing continental vertical motion histories since the Paleozoic. Earth Planet. Sci. Lett. 317, 426–435. doi:10.1016/j.epsl.2011.10.041
Zhong, S.J. (2002), Effects of lithosphere on the long-wavelength gravity anomalies and their implications for the formation of the Tharsis rise on Mars, J. Geophys. Res., 107, 5054, doi:10.1029/2001JE001589.
Zhong, S.J., McNamara, A., Tan, E., Moresi, L., Gurnis, M. (2008), A benchmark study on mantle convection in a 3-D spherical shell using CitcomS. Geochem. Geophys. Geosystems 9, Q10017. doi:10.1029/2008GC002048
Zhong, S. J., M. Ritzwoller, N. Shapiro, W. Landuyt, J. Huang, and P. Wessel (2007), Bathymetry of the Pacific Plate and its implications for thermal evolution of lithosphere and mantle dynamics, J. Geophys. Res., 112, B06412, doi:10.1029/2006JB004628
Zhong, S., and M. Gurnis (1994), The role of plates and temperature-dependent viscosity in phase change dynamics, J. Geophys. Res., 99, 15,903-15,917. <references />